Las bobinas y condensadores, son elementos que tienen un comportamiento variable segun la frecuencia. Las bobinas, por su parte, tienen una reactancia proporcional a la frecuencia, Z = jwL, mientras que los condensadores son inversamente proporcionales a ésta, Z=1/jwC.
Si la frecuencia tiende a 0 (continua), las bobinas se comportan como un cortocircuito, mientras que los condensadores como un circuito abierto. Por otro lado, si la frecuencia tiende a infinito, las bobinas serán las que se comportan como un circuito abierto, mientras que los condensadores como un cortocircuito.
Podemos entender, por lo tanto, a una bobina como un filtro paso-bajo, y a un condensador como un filtro paso-alto.
Circuito tanke LC:
Si conectamos un condensador en serie con una bobina (circuito tanke LC), formando un divisor de tensión con un generador y su resistencia interna, obtendremos un comportamiento paso-bando. El análisis es el siguiente; en bajas frecuencias, la bobina dejará pasar el corriente, y en altas lo dejará pasar el condensador, siendo Vo = 0. Analizando la función de transferencia del circuito, vemos que hay una frecuencia, en la que el divisor de tensión tendrá una amplificación máxima. A ésta se la conoce como frecuencia de resonancia fr, y corresponde a fr = 1/(2·pi·sqrt(L·C)).
La caildad del pico de resonancia se puede medir como Q = fr/BW, que en radianes es
Q = wr/BW = R·sqrt(C/L).
Éste analisis se puede extender a muchos circuitos paso banda, agrupando las resistencias, capacitores e inductores.
Bipolo RLC:
Otro circuito de importancia es el bipolo RLC.
La impedancia de éste, tendrá un comportamiento igual que el del filtro paso-banda. En el pico de resonancia, la impedancia corresponderá a R. Por lo tanto el bipolo RLC, se comporta como un resistor de impedáncia variable en frecuencia
Su pico de resonancia y BW, serán los mismos que en el circuito divisor de tensión anterior, con BW=1/(2·pi·R·C) y fr=1/(2·pi·sqrt(L·C)).
Circuito resonante con Rserie;
En la realidad, las bobinas, al ser un hilo largo y estrecho devanado, presentan una resistencia, como R = pL/S, siendo p la resistividad, L la longitud, y S al sección.
Por lo tanto, en un circuito tank LC, podemos analizar la bobina como un inductor ideal, en serie con una resisténcia parásita Rs. Mediante análisis del circuito, podemos transformar esta resistencia en serie Rs, en una resistencia en paralelo Rp, siendo Rp = 1/Rs·C, y obteniendo así un bipolo RLC, o RpLC.
Finalmente, llegamos a la conclusión, que si conectamos el circutito resonante Rserie a un generador con su resistencia interna Rg, lo convertimos en el circuito bipolo RLC, con R = Rp = 1/Rs·C, y juntamos las resistencias Rg con Rp (equivalente en paralelo), podemos obtener su curva de filtro paso-banda, con su frecuencia de resonancia y su BW.
Una vez ya sabemos como analizar los circuitos tank, éstos tienen muchísimas utilidades. Por ejemplo, podemos convertir un amplificador inversor en un filtro paso-banda, substituyendo R2 por el circuito tank, o realizar un amplificador sintonizado mediante un transistor.
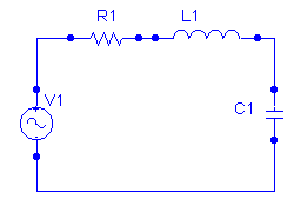
Circuito serie RLC:
Otra estructura hábil para crear picos de resonancia, es el circuito serie RLC. Conectando una bonia en serie con un condensador, formando un divisor de tensión, vemos que la curva ideal al excitar el circuito, la de un filtro paso-banda, con una asímptota en la frecuencia de resonancia.
Al no existir generadores ideales sin ninguna resistencia interna Rg, el circuito en la práctica, se basa en una resistencia Rg, en serie con una bobina, conectados con un condensador también en sèrie, formando un divisor de tensión.
fr = 1/(2·pi·sqrt(L·C)), pero con el BW que depende de la bobina, BW = R/(2·pi·L).
El factor de calidad del picos en este caso, queda Q = fr/BW = (1/R)·sqrt(C/L).
Cap comentari:
Publica un comentari a l'entrada